
알아보기
Depth-First Search 깊이 우선 탐색이다.
임의의 노드에서 시작하여 다음 분기로 넘어가기 전까지 해당 분기를 끝까지 탐색하는 방법이다.

미로를 탐색할 때 한 방향으로 쭉 가다가(깊이) 갈 수 없는 상황이 되면, 그 전 노드로 돌아와(**백트래킹**) 인접한 다른 노드를 탐색하고, 그 노드 아래에 있는 노드들을 쭈욱 탐색하는 경우가 dfs를 사용하는 예라고 볼 수 있다.
따라서, 어떤 노드를 방문했었는지 반드시 체크하여 검사를 해야한다.
그렇지 않으면 무한 루프에 빠질 수도 있다.
적용하기
미로 탐색뿐만아니라, 순열, 중복순열,조합,메모이제이션에서도 응용이 가능하다.
순열
예를 들어 1~N까지의 자연수 중 M개를 뽑아 일렬로 나열하는 경우의 수가 순열이다.
N=3, M=2이라고 가정하면,
{3,6,9} 배열에서 {3,6},{3,9},...,{9,3}
말그대로 순열 이므로, 같은 조합이지만 순서가 다르다면 다른 경우로 취급한다.
당연히 같은 숫자가 들어가면 안되기 때문에 이미 사용했는지 체크를 해주어야한다.
dfs 적용해보기
m개를 뽑는다면 m개 크기의 조합 배열(pm), 숫자가 쓰였는지 확인하는 체크배열을 생성한다.

중복순열
순열과 다른점은 중복이 허락된다는 점이다.
1부터 N까지의 자연수 중 중복을 허락하여 M개를 뽑아 나열하는 경우의 수이다.
위의 예시를 든다면
{1,1},{1,2},{1,3},{2,1}...{3,3}
dfs 적용해보기
m개를 뽑는다면 m개 크기의 조합 배열(pm)을 생성한다.

조합
조합은 순열과 다르게 순서의 구분이 없다는 것이다.
위의 예시를 든다면
{1,2},{1,3},{1,4} ...
같은 수가 들어간 {1,1} 이나 이미 {1,4}가 나왔던 조합인 {4,1}은 카운트하지 않는다.
dfs 적용해보기

메모이제이션
조합의 경우의 수를 구하는 공식은 아래와 같다.

이를 dfs를 적용해본다면
public static int dfs(int n, int r){
if(n == r || r== 0){
return 1;
}else{
return dfs(n-1,r-1)+dfs(n-1,r-1);
}
}하지만 매번 함수를 리턴해야해서 스택 부담이 크고, 값이 커질수록 시간도 늘어난다.
메모이제이션을 사용해보자. 메모이제이션이란, 결과를 도출하는 과정에서 나오는 중간값을 저장하여, 해당 값만 참조하면 되는 장점이 있다.

2차원배열(memo)을 생성하고 가령 3C1이라면 memo[3][1] = 3 을 넣어준다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static int[][] memo = new int[35][35];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int r = Integer.parseInt(st.nextToken());
System.out.println( dfs(n,r));
}
public static int dfs(int n, int r){
if(memo[n][r]>0) return memo[n][r];
if(n == r || r== 0){
return memo[n][r]=1;
}else{
return memo[n][r] = dfs(n-1,r-1)+dfs(n-1,r);
}
}
}
말단 노드까지의 가장 짧은 경로를 구해보자.
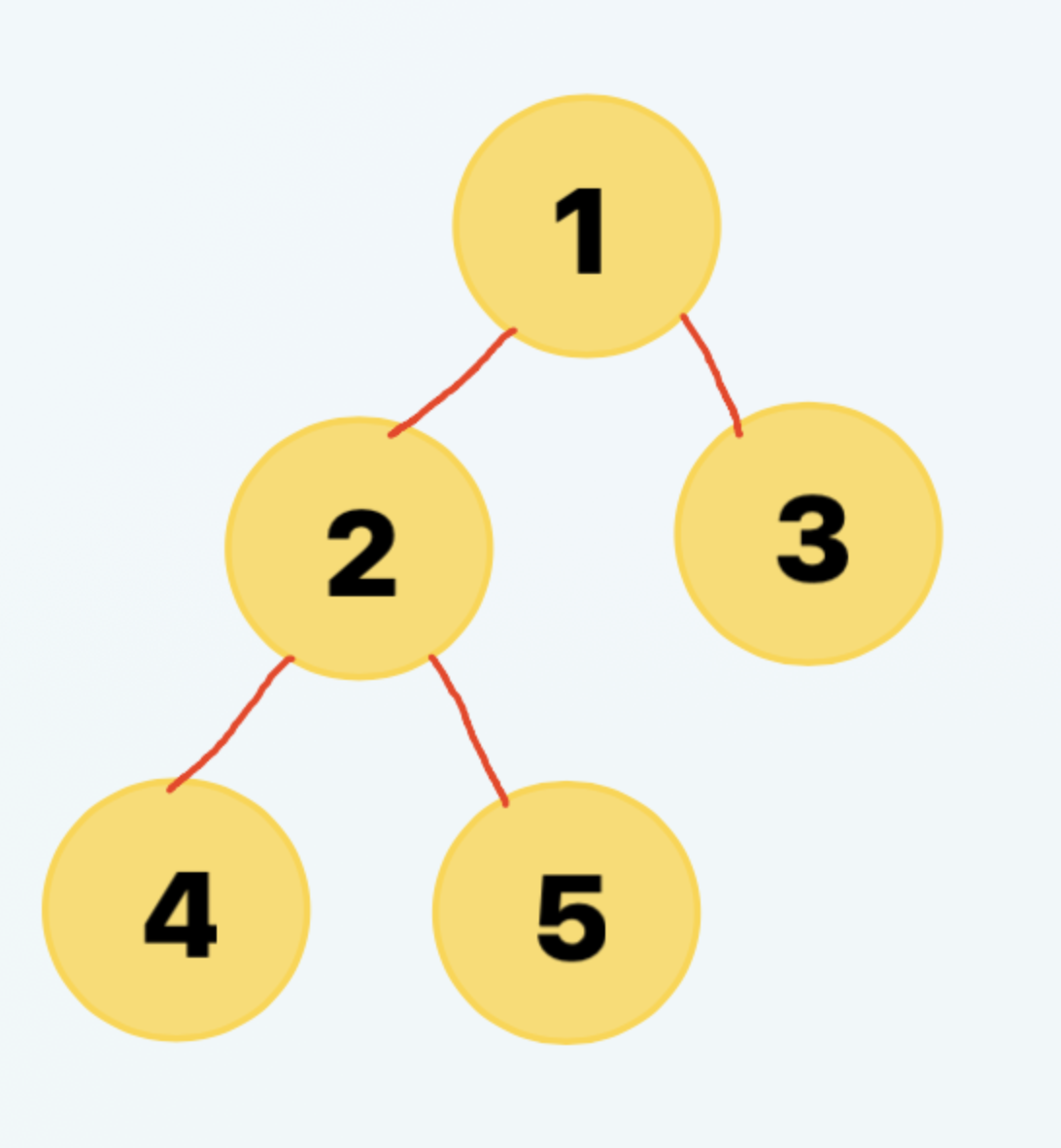
위의 그래프를 dfs 방법으로 탐색하여 말단노드까지의 최소경로를 구해보자.
class Node{
int data;
Node lt,rt;
Node(int val){
this.data = val;
lt = rt = null;
}
}
public class Main {
Node root;
public int dfs(int L, Node root){
if(root.lt == null && root.rt == null){
return L;
}else{
return Math.min(dfs(L+1,root.lt), dfs(L+1,root.rt));
}
}
public static void main(String[] args) {
Main tree = new Main();
tree.root = new Node(1);
tree.root.lt = new Node(2);
tree.root.rt = new Node(3);
tree.root.lt.lt = new Node(4);
tree.root.lt.rt = new Node(5);
System.out.println(tree.dfs(0,tree.root));
}
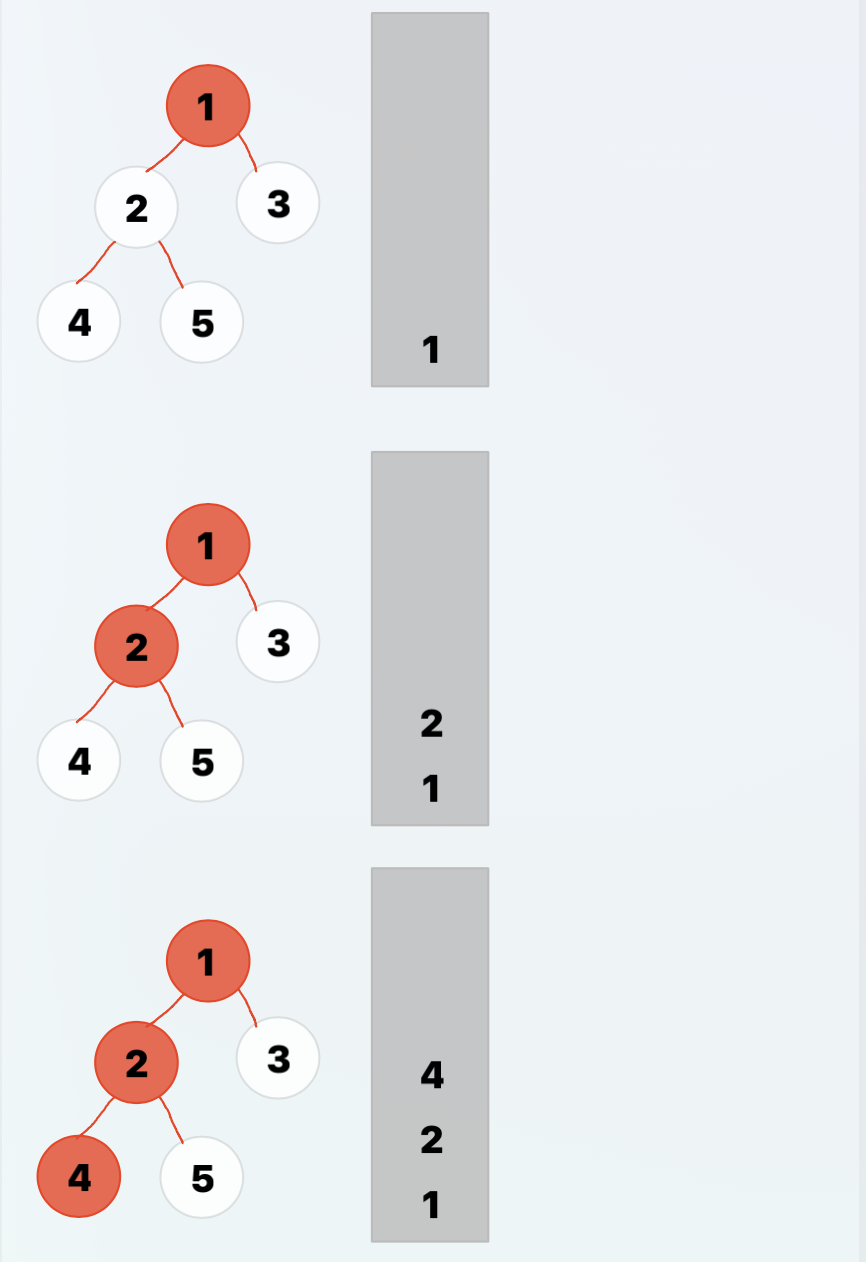
}그래프 탐색과, 코드가 스택에 쌓이는 과정을 그림으로 나타내 보았다.


'코딩테스트 > 알고리즘' 카테고리의 다른 글
| Dynamic Programing 다이나믹 프로그래밍 (0) | 2023.11.06 |
|---|---|
| Greedy 그리디 (0) | 2023.11.06 |
| Daijkstra 다익스트라: 과정 이해하고 적용해보기 (1) | 2023.11.03 |
| BFS 너비 우선 탐색: 과정 이해하고 적용해보기 (0) | 2023.11.02 |
| Graph 그래프 (1) | 2023.11.01 |