
알아보기
다익스트라 알고리즘은
가중치 그래프에서 가중치의 값이 모두 양수일 때 한 노드에서 각 노드까지의 최소거리를 구할때 사용한다.
방문한 노드들을 체크하여, 체크하지 않은 노드들 중 가장 비용이 적은 노드를 선택(그리디)하고,
그 비용과 기존의 비용을 비교하여 값을 갱신(프로그래밍)하는 방식이다.

적용해보기
위의 그래프를 이용하여 1번 노드에서 각 노드까지의 최소비용 구해보도록 하자.
각 노드로 가는 최소 비용을 담는 배열 dis을 생성한다.
그 값들은 최대값으로 일단 해놓고, 1번정점을 0으로 한 뒤 시작한다.
배열 값 중 0의 값이 최소이므로 체크해 놓고, 1번노드에서 바로 갈 수 있는 노드에 대한 비용을 각 노드가 가진 현재 값과 비교하여 더 작다면 바꾼다.
체크하지 않은 노드들 중 가장 최솟값을 가진 노드에서부터 바로 갈 수 있는 노에 대한 비용을 현재 값과 비교하여 더 작다면 바꾼다.
글로는 이해가 어려우니 그림으로 그려보았다.

이 방법은 노드의 개수가 N일때 체크되지 않은 값 중, 최솟값을 찾을 때 O(N)의 시간 복잡도가 발생하므로 최종적으로
(N-1) * O(N) 의 복잡도가 발생한다.
N이 1000이라면 1000000 이고, 그 이상이면,,,,,🙄
PriorityQueue를 이용하기
최솟값을 찾는 시간을 줄이기 위하여 우선순위 큐를 사용해보자.
우선순위 큐는 logN의 시간복잡도를 가지고 있기 때문에 최종적으로 (N-1)*logN의 값이 나온다.
N이 1000이라면 1000*3 이므로 위의 방법보다 훨씬 시간복잡도가 적다.
그렇다면 PriorityQueue(이하 pq)를 이용하는 방법을 그림으로 알아보겠다.
먼저 최소거리배열, 그래프의 정보를 담을 리스트 배열, 정점과 그 정점으로 가는 비용을 정의할 Edge 객체를 생성해준다.

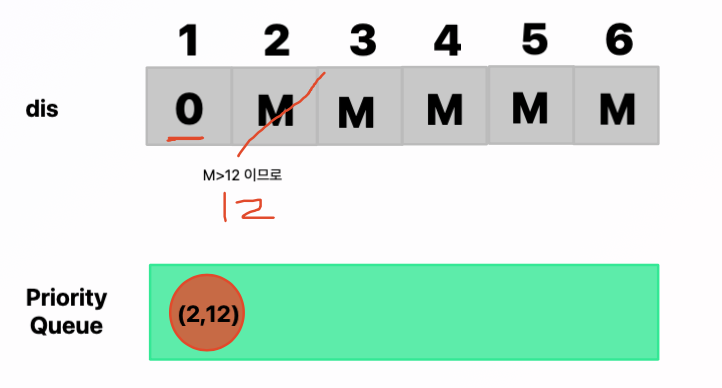
1번 노드를 pq에 넣는것과 dis[1]=0으로 바꾸는것부터 시작한다.

pq에 있는 Edge 객체를 꺼내면 정점과 인접한 정점들을 꺼내올 수 있다.

ArrayList<Edge> = graph.get(1);2번 정점으로는 비용이 12가 발생하므로 M보다 작기때문에 거리 배열에 12로 바꾸고
2번 정점과 12를 엣지 객체를 생성하여 pq에 넣는다.
3번 정점으로는 비용이 4가 발생하므로 M보다 작기때문에 거리 배열에4로 바꾸고
3번 정점과 4를 엣지 객체를 생성하여 pq에 넣는다.

만약, 정점으로 가는 비용이 현재 배열에 들어있는 값보다 같거나 크다면 continue를 한다.
이 로직을 pq가 비어있을때까지 반복한다.



결과

'코딩테스트 > 알고리즘' 카테고리의 다른 글
| Dynamic Programing 다이나믹 프로그래밍 (0) | 2023.11.06 |
|---|---|
| Greedy 그리디 (0) | 2023.11.06 |
| BFS 너비 우선 탐색: 과정 이해하고 적용해보기 (0) | 2023.11.02 |
| DFS 깊이 우선 탐색: 과정 이해하고 적용해보기 (0) | 2023.11.01 |
| Graph 그래프 (1) | 2023.11.01 |